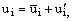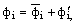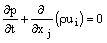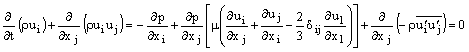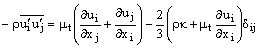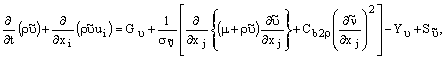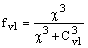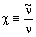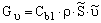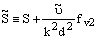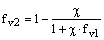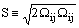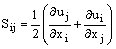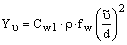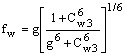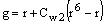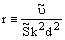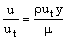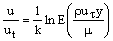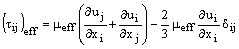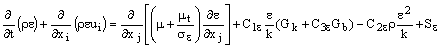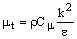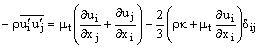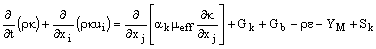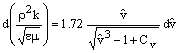Раздел 10. Модели турбулентности
[...]
Секция 10.1: Введение.
Секция 10.2: Выбор модели турбулентности.
Секция 10.3: Модель "Spalart-Allmaras".
Секция 10.4: "Standard", "RNG", "Realizable" k-e модели.
Секция 10.5: "Standard" k-w, "SST" k-w модели.
Секция 10.6: Модель "RSM".
Секция 10.7: Модель "LES".
Секция 10.8: Моделирование погранслоя в турбулентном потоке.
Секция 10.9: Рекомендации к расчетным сеткам при моделировании турбулентных течений.
Секция 10.10: Постановка задачи при расчете турбулентных течений.
Секция 10.11: Методика постановки задачи при моделировании турбулентных течений.
Секция 10.12: Обработка результатов расчета турбулентных течений.
Турбулентные потоки характеризуются пулсационной составляющей скорости. Эти пульсации перемешивают параметры переноса потока (импульса, энергии, и параметры концентрации), что приводит к пульсации самих параметров переноса. Так как эти пульсации могут быть мелкомасштабными и высокочастотными, моделирование такого процесса с помощью прямого численного моделирования требует огромных вычислительных ресурсов. Вместо этого полные уравнения движения осредняют по времени, по пространству или используют другие способы исключения локальных мелкомасштабных пульсаций, получая измененные уравнения движения, которые более приемлимы для промышленных расчетов. Однако, полученные уравнения движения имеют дополнительные неизвестные переменные, для определения этих переменных используются модели турбулентности.
FLUENT предлагает на выбор следующие модели турбулентности:
- Model Spalart-Allmaras
- k-e модели
- Стандартная k-e модель "Standard k-e"
- Ренормализационная k-e модель "RNG k-e"
- Реализованная k-e модель "Realizable k-e" - k-w модели
- Стандартная k-w модель "Standard k-w"
- Модель k-w с переносом касательных напряжений "SST k-w" - Модель Рейнольдсовых напряжений "RSM"
- Модель больших вихревых структур "LES"
10.2 Выбор модели турбулентности
К сожалению, на данный момент не существует универсальной модели турбулентности для широкого диапазона течений. Выбор модели турбулентности зависит от характера турбулентного потока, требуемой точности, доступных вычислительных ресурсов, и временных затрат необходимых на процесс моделирования. Для адекватного выбора модели турбулентности необходимо четко представлять свойства и ограничения каждой модели турбулентности.
Основной целью данного раздела является краткий обзор моделей турбулентности предлагаемых FLUENT, а также требуемые ими вычислительные ресурсы: время центрального процессора, оперативная память. Практически невозможно дать стопроцентную рекомендацию по выбору модели турбулентности в определенных промышленных областях, но можно представить основные критерии выбора, которые помогут вам определиться с моделью турбулентности для решаемой вами задачи.
Нестационарное решение точных уравнений Навье-Стокса для сложных потоков с большим числом Рейнольдса на данный момент является невозможным. Существует два альтернативных способа представления уравнений Навье-Стокса в которых не учитываются мелкомасштабные турбулентные пульсации: метод осреднения по правилам Рейнольдса и метод фильтрации. Обе методики требуют дополнительных уравнений для замыкания всей системы.
Метод осреднения уравнений Навье-Стокса имеет английскую абривиатуру "RANS" (Reynolds-averaged Navier-Stokes) и предполагает запись уравнений переноса осредненного по времени потока, со всеми предполагаемыми масштабами турбулентности. Такой подход значительно уменьшает вычислительные ресурсы, необходимые для решения численной задачи. В том случае, если осредненный поток является стационарным, то основные уравнения не содержат производных по времени и установившееся решение получается более экономичным. Вычислиельное приемущество наблюдается даже для случая переходных режимов, т.к. шаг по времени определяется глобальной неустойчивостью осредненного потока, а не турбулентностью. Метод осреднения уравнений Навье-Стокса в основном применяется в промышленности для решения инженерных задач, и используется в таких моделях турбулентности, как: "Spalart-Allmaras", k-e и ее разновидностях, k-w и ее разновидностях, модели Рейнольдсовых напряжений "RSM".
Модель больших вихревых структур имеет английскую аббревиатуру "LES" (Lage Eddy Simulations) и использует альтернативный подход, в котором большие вихри решены в нестационарной постановке с использованием системы, так называемых, «фильтрующих» уравнений. Набор «фильтрующих» уравнений по существу служит для исключения из расчета подсеточных вихрей, т.е. вихрей размер которых меньше ячеек расчетной сетки. Как и в случае осреднения по Рейнольдсу процесс фильтрации требует добавления специальных уравнений для замыкания всей системы. Статистические величины осредненного потока, которые в основном и имеют практический интерес, представляются в зависимости от времени. Привлекательность "LES" модели заключается в том, что он рассчитывает потери вызванные самим режимом турбулентного течения, в отличие от моделей турбулентности относящихся к классу "RANS". Возможно это качество делает ее «универсальной» для расчета турбулентных течений с тенденцией мелкомасштабных вихрей, что имеет место в ярко выраженных изотропных потоках, т.е. когда макроскопические особенности потока преобладают над крупномасштабными вихрями.
Стоит подчеркнуть, что применение "LES" модели в промышленных задачах крайне ограничено. Эта особенность была выдвинута на первый план в публикации [72], типичное приминение данной модели было найдено лишь в достаточно простых геометрических областях, что в основном связано с высокими требованиями данной модели к вычислительным ресурсам. "LES" модель использует пространственную дискретизацию высокого порядка, что позволяет разрешить больший диапозон масштабов турбулентности. Но имеет место, ухудшенная точность решения осредненных параметров потока в "LES" модели, что не всегда документируется. В добавление, стоит отметить, что использование пристеночных функций с "LES" моделью требует дальнейшей ратификации.
Таким образом, можно сделать выводы, что для практических расчетов рекомендуется использовать класс моделей "RANS". "LES" подход, описанный в дальнейшем в секции 10.7, доступен во FLUENT, но еще раз стоит отметить, что он требует больших вычислительных ресурсов. Данный же раздел посвящен выбору моделей турбулентности представленных в классе "RANS" моделей.
10.2.2 Осреднение по правилам Рейнольдса
Для количественного описания развитого турбулентного движения Рейнольдс предложил следующий, получивший широкое применение прием. Мгновенные параметры решения в точных уравнениях Навье-Стокса разделяются на осредненные и пульсационные составляющие. Для компонент скорости:
|
|
10.2-1 |
где 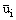 и
и 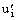 - осредненная во времени и пульсационная
(отклонение действительных скоростей от осредненных) составляющая (i=1,2,3).
- осредненная во времени и пульсационная
(отклонение действительных скоростей от осредненных) составляющая (i=1,2,3).
Аналогично для давления и других скалярных величин:
|
|
10.2-2 |
где 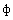 - такие скаляры, как давление, энергия, или разновидности концентрации.
- такие скаляры, как давление, энергия, или разновидности концентрации.
В дальнейшем предполагается, что в развитом турбулентном движении пульсации малы по сравнению со средними скоростями потока.
Подставляя приведенные выше выражения в уравнение неразрывности и уравнение импульса получаем (запись в виде тензора в цилиндрической системе координат):
|
|
10.2-3 |
|
|
10.2-4 |
Уравнения 10.2-3 и 10.2-4 – осредненные по Рейнольдсу уравнения Навье-Стокса. Они записаны в общей форме, также, как и точные уравнения Навье-Стокса, только теперь скорости и другие переменные решения записаны в виде осредненных величин.
Появились дополнительные параметры вызванные эффектом турбулентности. Это Рейнольдсовые напряжения,
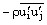 , которые необходимы для замыкания уравнения 10.2-4.
, которые необходимы для замыкания уравнения 10.2-4.
Для сжимаемых потоков, уравнения 10.2-3 и 10.2-4 должны быть интерпретированы как уравнения Навье-Стокса осредненные по методу Фейвра [91], со скоростями представленными осредненными по массовому расходу.
10.2.3 Метод Буссинеска против метода переноса Рейнольдсовых напряжений
Метод осреднения по Рейнольдсу для моделирования турбулентности требует решения Рейнольдсовых напряжений в уравнении 10.2-4. Обычно используется гипотеза Буссинеска [91], которая связывает Рейнольдсовые напряжения с осредненными градиентами скоростей:
|
|
10.2-5 |
Гипотеза Буссинеска используется в моделях турбулентности "Spalart-Allmaras", k-e
моделях, k-w моделях. Преимущество этой методики заключается в небольших вычислительных ресурсах,
что объясняется способом вычисления турбулентной вязкости 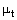 . В модели
"Spalart-Allmaras" решается только одно уравнение переноса для турбулентной вязкости. В случае k-e
и k-w моделей решается два дополнительных уравнения переноса (для турбулентной кинетической
энергии, k, и скорости турбулентной диссипации, e, или специфической скорости диссипации,
w), а турбулентная вязкость,
. В модели
"Spalart-Allmaras" решается только одно уравнение переноса для турбулентной вязкости. В случае k-e
и k-w моделей решается два дополнительных уравнения переноса (для турбулентной кинетической
энергии, k, и скорости турбулентной диссипации, e, или специфической скорости диссипации,
w), а турбулентная вязкость, 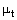 , вычисляется, как
функция k и e. Недостатком гипотезы Буссинеска является то, что водится предположение о
изотропности турбулентной вязкости, что строго говоря не всегда верно.
, вычисляется, как
функция k и e. Недостатком гипотезы Буссинеска является то, что водится предположение о
изотропности турбулентной вязкости, что строго говоря не всегда верно.
Альтернативный подход, воплощенный в модели Рейнольдсовых напряжений "RSM", состоит в том, что уравнения переноса соответствующих величин решается с помощью тензора Рейнольдсовых напряжений. В качестве дополнительного уравнения используется уравнение переноса для скорости турбулентной диссипации e, которое необходимо для определения масшатаба турбулентности. Это означает, что для двумерных задач требуется 5 дополнительных уравнений переноса, а для трехмерных 7.
Во многих случаях, модели основанные на гипотезе Буссинеска работают достаточно хорошо, и использование "RSM" модели является неоправданным с точки зрения вычислительных затрат. Однако модель "RSM" незаменима в ситуациях, когда анизотропность турбулентного потока оказывает доминируещее влияние на осредненный поток. Это встречается в высокоскоростных вращающихся потоках и потоках с развитыми вторичными течениями, вызванными неоднородностью поля напряжений.
10.2.4 Модель "Spalart-Allmaras"
Эта модель турбулентности является относительно простой, с одним дополнительным уравнением переноса турбулентной вязкости, что воплощает относительно новый класс однопараметрических моделей, в которых нет необходимости вычислять длину пути смешения, связанного с локальной толщиной слоя, характеризующегося большими значениями касательных напряжений. Модель "Spalart-Allmaras" была специально разработана для аэрокосмической промышленности и показала хорошие результаты решения пограничных слоев, подверженных неблагоприятным градиентам давления, а в последнее время все более широкое применение находит в области турбомашиностроения.
Оригинальная форма модели "Spalart-Allmaras" рассматривалась, как модель турбулентности для потоков с низким числом Рейнольдса, которая требовала хорошего сеточного разрешения в области пограничного слоя. Во FLUENT эта модель была реализована таким образом, что в случае плохого разрешения пристеночной области используются пристеночные функции. В таком случае эта модель является хорошим выбором для задач с грубой сеткой. Кроме того, градиенты турбулентной вязкости в пристеночных областях в таком случае значительно меньше чем градиенты переносимых переменных в моделях турбулентности k-e и k-w. Это делает модель менее чувствительной к численным ошибкам, когда в пристеночной области величина градиента размеров ячеек меняется не плавно, т.е. сетка обладает низким коэффициентом сглаженности. Более подробно об описании численных ошибок смотрите секцию 5.1.2.
Однако, модель "Spalart-Allmaras" является относительно новой и ее использование для широкого класса турбулентных потоков является еще не аппробированным. Использование этой модели турбулентности не рекомендуется для предсказания гомогенной, изотропной турбулентности. Кроме того одно-параметрические модели турбулентности часто критикуются за их неспособность быстро приспосабливаться в случае изменения масштаба длины, что необходимо когда течение резко переходит из пристеночной области в область свободную от касательных напряжений, т.е. при наличии в потоке зон отрыва пограничного слоя.
Простая двухпараметрическая модель турбулентности, в которой решаются два уравнения переноса определяющие турбулентную скорость и масштаб длины. Стандартная k-e модель представленная во FLUENT получила широкое применение в решении практических инженерных задач, с тех пор, как она была предложена Лаундером и Сполдингом [128]. Ошибкоустойчивость, экономичность, и разумная точность для широкого диапозона турбулентных потоков делает ее наиболее применимой в промышленных задачах. Постоянные коэффициенты для этой модели турбулентности получены опытным путем и поэтому она является полуэмпирической. На базе стандартной k-e с учетом ее недостатков были созданы "RNG" k-e модель [272] и "Realizable" k-e модели [209].
"RNG" k-e модель была разработана на основе строгих статистических методов (renormalization group theoy). Она аналогична стандартной k-e модели, но имеет ряд существенных отличий:
- Дополнительное условие в уравнении скорости турбулентной диссипации e улучшает точность решения высоконапряженных потоков.
- Дополнительный параметр, учитывающий циркуляцию турбулентности, улучшает точность расчета течений с закруткой потока.
- "RNG" теория предлагает аналитическую формулу турбулентных чисел Прандтля, в то время, как в стандартной k-e модели данный параметр является константой.
- В то время, как стандартная k-e модель является высокорейнольдсовой моделью, RNG теория предоставляет полученную аналитическим путем дифференциальную формулу эффективной вязкости, что более приемлимо при расчете низкорейнольдсовых течений. Но стоит отметить, что данная формула работает при качественном сеточном разрешении в области пограничного слоя.
Эти особенности делают RNG k-e модель более точной и надежной для широкого диапозона турбулентных течений, чем в случае со стандартной k-e моделью.
10.2.7 "Realizable" k-e модель
Данная модель была относительно недавно разработана и отличается от стандартной k-e модели:
- Улучшенная форма записи турбулентной вязкости.
- Новое уравнение переноса скорости диссипации, e, получено из точного уравнения переноса среднеквадратичного пульсационного вихря.
Термин "Realizable" означает, что модель разрешает некоторые математические ограничения Рейнольдсовых напряжений, которые имеют место в турбулентных течениях. Непосредственное преимущество "Realizable" k-e модели состоит в том, что она более точно предсказывает распределение диссипации плоских и круглых струй. Это также вероятно обеспечит более лучшее предсказание вращающихся потоков, пограничных слоев подверженных сильным градиентам давления, отрывных течений и рециркуляционных течений. Обе модели "Realizable" и "RNG" k-e показывают существенное преимущество перед стандартной k-e моделью турбулентности для искривленных, вихревых и вращающихся потоков. "Realizable" k-e модель является еще достаточно новой и не была проведена полная ее аппробация для широкого диапозона турбулентных потоков, но по своей постановке является более предпочтительной. Начальные практические исследования показали ее явное превосходство при решении потоков, характеризующихся отрывными течениями и потоков в которых имеют место развитые вторичные течения.
У "Realizable" k-e модели турбулентности существует недостаток, который заключается в том, что она завышает или занижает турбулентную вязкость потока, когда вычислительная область содержит одновременно вращающиеся и неподвижные области (т.е. при использовании множественных систем координат или скользящих сеток). Это объясняется тем, что модель использует эффект осредненного вращения при определении турбулентной вязкости (смотрите уравнения 10.4-14-10.4-19). Этот подход был протестирован для случая одинарной вращающейся системы координат и результаты показали более точное решение, чем в случае стандартной k-e модели турбулентности. Однако, использование этой модели для множественных систем координат является остается под некоторым вопросом.
Стандартная k-w модель во FLUENT основана на модели Уилкокса [267], которая адаптирована для расчета течений с низким числом Рейнольдса, сжимаемости и течений с отрывом пограничного слоя. Показывает отличные результаты расчета пристеночных слоев и потоков с низким числом Re. Разновидностью стандартной k-w модели является SST k-w модель, которая также доступна во FLUENT, и описана в секции 10.2.9.
10.2.9 Модель переноса касательных напряжений "SST" k-w
Данная модель имеет англоязычную аббревиатуру "SST" (Shear-Stress Transport), является разновидностью стандартной k-w модели и была разработана Ментером. Даная модель эффективно сочетает устойчивость и точность стандартной k-w модели в пристеночных областях и k-e модели на удалении от стенок, для этого k-e модель была конвертирована в k-w модель. "SST" k-w модель имеет следующие особенности по сравнению со стандартной k-w моделью:
- Стандартная k-w модель и преобразованная k-e модель объединяются специальной функцией и обе добавлены в представленную модель. Специальная функция в пристеночной области принимает значение единицы, активизируя стандартную k-w модель, а на удалении от стенки принимает значение нуля, активизируя преобразованную k-e модель.
- Определение турбулентной вязкости модифицировано для представления уравнения переноса касательных напряжений.
- Отличаются константы моделей турбулентности.
Эти особенности делают SST k-w модель более точной и надежной для широкого класса потоков (т.е., потоков подверженных градиентам давления, обтекание профилей, околозвуковые ударные волна), чем в случае стандартной k-w модели.
10.2.10 Модель Рейнольдсовых напряжений "RSM"
Модель Рейнольдсовых напряжений имеет англоязычную аббревиатуру "RSM" (Reynolds Stress Model) и является одной из самых сложных моделей турбулентности предлагаемых FLUENT. Эта модель не использует предположение о изотропности турбулентной вязкости, а для замыкания уравнений Навье-Стокса, осредненных по Рейнольдсу, решает уравнения переноса для Рейнольдсовых напряжений совместно с уравнением для скорости турбулентной диссипации e.
Так как модель "RSM" описывает эффекты кривизны, закрученности, вращения, резкого изменения напряжений между слоями более строго, чем одно- и двух- параметрические модели турбулентности, то она имеет больший потенциал для более точного расчета сложных потоков. Однако "RSM" модель все-таки имеет некоторые упрощения, которые были приняты для составления уравнений переноса Рейнольдсовых напряжений. Использование этой модели турбулентности рекомендуется в случаях, когда анизотропность турбулентного потока оказывает доминируещее влияние на характер турбулентного течения (циклоны, сильно закрученные потоки в камерах сгорания, вращающиеся области, вторичные течения в каналах, вызванные большими нормальными напряжениями и т.д.).
С точки зрения вычислительных ресурсов, модель турбулентности "Spalart-Allmaras" является самой экономичной, т.к. она использует одно доплонительное уравнение переноса турбулентной вязкости.
Стандартная k-e модель требует несколько больших вычислительных ресурсов по сравнению с моделью "Spalart-Allmaras", т.к. описывается двумя дополнительными уравнениями переноса. "Realizable" k-e модель требует несколько больших вычислительных усилий по сравнению со стандартной k-e моделью, из-за дополнительных условий и функций в основных уравнениях, а также из-за большей степени нелинейности. Вычисления с помощью "RNG" k-e модели занимает на 10-15% времени центрального процессора больше, чем в случае стандартной k-e модели. Подобно k-e моделям, k-w модели также являются двух-параметрическими и требуют некоторых вычислительных усилий.
По сравнению с k-e и k-w моделями турбулентности "RSM" требует дополнительную память и время центрального процессора из-за увеличения числа уравнений переноса Рейнольдсовых напряжений. В среднем "RSM" требует на 50-60% времени CPU больше, чем двух-параметрические модели турбулентности и на 15-20% больше оперативной памяти.
Кроме временных затрат на итерационный процесс, выбор модели турбулентности может повлиять на сходимость численного решения. Например, стандартная k-e модель, как известно является в некоторых случаях сверхдиффузионной, в то время, как RNG k-e модель разработана такой, что турбулентная вязкость уменьшается при резких изменениях напряжений. Так как диффузия положительно влияет на сходимость численного решения, то вероятно, что RNG k-e модель будет более восприимчивой к неустойчивости в стационарных задачах. Однако, это не является недостатком RNG k-e модели, т.к. эта характеристика делает ее более отзывчивой к физической нестабильности, такой как временнозависимые потери турбулентных вихрей.
Точно также и "RSM" модель может потребовать большего количества итераций по сравнению с двух-параметрическими моделями, т.к. в ней заолжена ярко выраженная взаимосвязь между Рейнольдсовыми напряжениями и осредненным потоком.
10.3 Модель "Spalart-Allmaras"
В моделях турбулентности, которые используют теорию Буссинеска, основная проблема возникает при вычислении вязкого вихря. Модель предложенная Спалартом и Аллмарасом [226] решает уравнения переноса параметров, которые изменяются турбулентной кинетической вязкостью.
10.3.1 Уравнение переноса в модели "Spalart-Allmaras"
Параметр переноса в модели "Spalart-Allmaras", 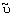 ,
идентичен турбулентной кинетической вязкости кроме пристеночных (подверженных молекулярной вязкости) областей.
Уравнение переноса
,
идентичен турбулентной кинетической вязкости кроме пристеночных (подверженных молекулярной вязкости) областей.
Уравнение переноса 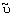 выглядит:
выглядит:
|
|
10.3-1 |
где 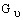 - производство турбулентной вязкости и
- производство турбулентной вязкости и
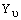 - распад турбулентной вязкости, который происходит в пристеночной области
из-за блокирования стенками вязкого демпфирования.
- распад турбулентной вязкости, который происходит в пристеночной области
из-за блокирования стенками вязкого демпфирования. 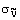 и
и
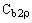 - константы и
- константы и 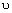 - молекулярная кинематическая вязкость.
- молекулярная кинематическая вязкость. 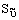 - заданный пользователем источник.
Следует отметить, что турбулентная кинетическая энергия k не рассчитывается в модели "Spalart-Allmaras", что не принято
во внмание при оценке Рейнольдсовых напряжений в уравнении 10.2-5.
- заданный пользователем источник.
Следует отметить, что турбулентная кинетическая энергия k не рассчитывается в модели "Spalart-Allmaras", что не принято
во внмание при оценке Рейнольдсовых напряжений в уравнении 10.2-5.
10.3.2 Моделирование турбулентной вязкости
Турбулентная вязкость, 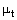 , определяется выражением:
, определяется выражением:
|
|
10.3-2 |
где функция вязкого демпфирования, 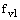 , определяется:
, определяется:
|
|
10.3-3 |
и
|
|
10.3-4 |
10.3.3 Моделирование производства турбулентности
Производство турбулентности, 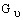 , определяется выражением:
, определяется выражением:
|
|
10.3-5 |
где
|
|
10.3-6 |
и
|
|
10.3-7 |
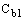 и k - константы, d - расстояние до стенки, и
S - скалярная мера тензора деформации. По умолчанию во FLUENT, как и в оригинальной модели предложенной
Спалартом и Аллмарасом, S базируется на величине завихренности:
и k - константы, d - расстояние до стенки, и
S - скалярная мера тензора деформации. По умолчанию во FLUENT, как и в оригинальной модели предложенной
Спалартом и Аллмарасом, S базируется на величине завихренности:
|
|
10.3-8 |
где 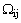 - тензор осредненной скорости вращения:
- тензор осредненной скорости вращения:
|
|
10.3-9 |
Выбор данной формулировки параметра S объясняется тем, что в потоках ограниченных стенками, которые вызывают практический интерес, турбулентность вызвана завихренностью вблизи стенок, которая, в свою очередь, вызвана самими стенками. Однако, общеизвестно, что в расчете необходимо учесть эффект осредненных напряжений вызванный производством турбулентности, что потребовало некоторой модификации модели, как предложено в [46] и доступно во FLUENT.
Эти модификации распространяются на тензоры вращения и напряжения при определении S:
|
|
10.3-10 |
где
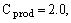
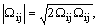
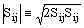
|
|
10.3-11 |
Тензоры вращения и напряжения уменьшают производство вязкого вихря и соответственно уменьшают саму вязкость вихря в областях, где величина завихрения превышает напряжения. В качестве примера можно привести вихревые течения, т.е., поток вблизи ядра вихря подвержен чистому вращению, где турбулентность, как известно подавлена. Тензоры вращения и напряжения более точно расчитывают эффекты вращения в турбулентных потоках. При установленной по умолчанию опции (включает только тензор вращения) наблюдается тенденция точного предсказания производства вязкого вихря, а следовательно и самого вязкого вихря.
Вы можете выбрать способ производства в панеле Viscous Model
10.3.4 Моделирование распада турбулентности
Распад турбулентности определяется выражением:
|
|
10.3-12 |
где
|
|
10.3-13 |
|
|
10.3-14 |
|
|
10.3-15 |
Сw1, Сw2, и Сw3 - константы, и 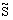 определяется уравнением 10.3-6. Следует отметить, что модификации описанные выше включают эффекты осредненного напряжения S,
также как и значение
определяется уравнением 10.3-6. Следует отметить, что модификации описанные выше включают эффекты осредненного напряжения S,
также как и значение 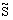 , используемое для расчета r.
, используемое для расчета r.
Постоянные модели 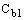
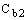
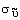
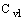
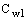
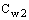
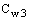 , и k имеют по умолчанию следующие значения [226]:
, и k имеют по умолчанию следующие значения [226]:
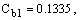
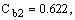
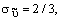
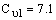
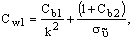
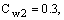
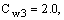

10.3.6 Пристеночные граничные условия
На стенках, модифицированная турбулентная кинетическая вязкость, 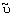 , равна нулю. Когда расчетная сетка достаточно
разрешеная для ламинарного подслоя, касательное напряжение на стенке получается из ламинарного деформационного-напряженного
равенства:
, равна нулю. Когда расчетная сетка достаточно
разрешеная для ламинарного подслоя, касательное напряжение на стенке получается из ламинарного деформационного-напряженного
равенства:
|
|
10.3-16 |
Если сетка неразрешает ламинарный подслой, подразумевается, что средняя точка пристеночного слоя ячеек лежит в логарифмической области пограничного слоя, тогда применяется следующий пристеночный закон:
|
|
10.3-17 |
где u -скорость параллельная стенке, ut - касательная составляющая скорости, y - расстояние до стенки, k - постоянная Кармана (0.4187), и E=9.793.
10.3.7 Моделирование конвективного теплообмена и переноса массы
Во FLUENT, турбулентный теплоперенос моделируется с использованием концепции аналогии Рейнольдса переносом турбулентного импульса. Таким образом моделирование уравнение энергии определяется следующим выражением:
|
|
10.3-18 |
k, в этом случае, тепловая проводимость, Е - полная энергия, и 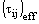 - тензор напряжения, определяемый выражением:
- тензор напряжения, определяемый выражением:
|
|
Параметр 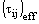 представляет вязкое нагревание, и всегда рассчитывается
совместными решателями. Он не вычисляется по умолчанию в последовательном решателе, но может быть установлен в панели
Viscous Model. По умолчанию турбулентное число Прандтля равно 0.85. Вы можете изменить это
значение в панели Viscous Model.
представляет вязкое нагревание, и всегда рассчитывается
совместными решателями. Он не вычисляется по умолчанию в последовательном решателе, но может быть установлен в панели
Viscous Model. По умолчанию турбулентное число Прандтля равно 0.85. Вы можете изменить это
значение в панели Viscous Model.
Турбулентный массоперенос рассмотрен также, с установленным по умолчанию турбулентным числом Шмидта 0.7. Это значение также может быть изменено в панели Viscous Model.
Пристеночные граничные условия для переноса скалярных величин "обрабатываются" аналогично импульсу, с использованием "пристеночного закона".
10.4 "Standard","RNG", и "Realizable" k-e модели
Все три модели имеют подобные формы, с уравнениями переноса k и e. Основное различие этих моделей заключается в следующем:
- Метод вычисления турбулентной вязкости.
- Турбулентные числа Прандтля управляющие турбулентной диффузией k и e.
- Генерация и распад параметров в e уравнении.
Уравнения переноса, методы вычисления турбулентной вязкости, и постоянные модели представлены раздельно для каждой модели. Особенности, которые, по существу, для всех моделей являются общими во всех моделях следующие: производство турбулентности, генерация вызванная плавучестью, эффекты сжимаемости, и моделирование тепло- и массопереноса.
Стандартная k-e модель турбулентности [128] является полу-эмпирической моделью, базирующейся на уравнениях переноса турбулентной кинетической энергии k и скорости диссипации e. Уравнение переноса k имеет точную формулировку, в то время как уравнение переноса для e выведено из физических рассуждений и имеет малое сходство с ее точной математической записью.
При выводе стандартной k-e модели вводилось предположение, что поток является полностью турбулентным (mt>>m), и таким образом эффекты вызванные молекулярной вязкостью незначительны, это говорит о том, что стандартная k-e модель справедлива только для полностью развитых турбулентных течений.
Уравнения переноса "Standard" k-e модели
Турбулентная кинетическая энергия, k, и скорость диссипации, e, представлены следующими уравнениями переноса:
|
|
10.4-1 |
|
|
10.4-2 |
В этих уравнениях, 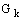 - производство турбулентной
кинетической энергии, вызванное градиентами осредненного потока, способ вычисления описан в секции 10.4.4.
- производство турбулентной
кинетической энергии, вызванное градиентами осредненного потока, способ вычисления описан в секции 10.4.4.
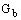 - производство турбулентной кинетической энергии, вызванное
плавучестью, способ вычисления описан в секции 10.4.5.
- производство турбулентной кинетической энергии, вызванное
плавучестью, способ вычисления описан в секции 10.4.5. 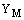 -
параметр характеризующий пульсации вызванные расширением в сжимаемых турбулентных потоках, рассчитывается,
как описано в секции 10.4.6.
-
параметр характеризующий пульсации вызванные расширением в сжимаемых турбулентных потоках, рассчитывается,
как описано в секции 10.4.6. 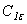 ,
,
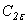 ,
,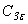 - эмпирические константы модели.
- эмпирические константы модели. 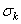 и
и
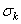 - турбулентные числа Прандля для k и e,
соответственно.
- турбулентные числа Прандля для k и e,
соответственно. 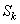 и
и 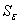 - источники определяемые пользователем.
- источники определяемые пользователем.
Моделирование турбулентной вязкости
Турбулентная (или вихревая) вязкость,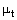 , является функцией
k и e, и определяется выражением Колмогорова-Прандля:
, является функцией
k и e, и определяется выражением Колмогорова-Прандля:
|
|
10.4-3 |
где 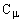 - эмпирическая константа.
- эмпирическая константа.
Константы модели
Константы модели 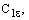

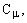
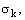
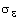 по умолчанию
имеют следующие значения:
по умолчанию
имеют следующие значения:
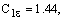
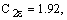
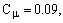
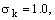
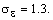
и были определены экспериментально для течения в области пограничного слоя и невозмущенных потоков (касательные напряжения достаточно малы), с учетом гомогенной изотропной подсеточной турбулентности.
Под гомогенной изотропной подсеточной турбулентностью подразумевают следующее. При выводе уравнений переноса турбулентных (Рейнольдсовых) напряжений часто пользуются гипотезой Буссинеска, связывающей турбулентные напряжения с градиентами осредненных скоростей турбулентного потока:
|
|
Недостатком гипотезы Буссинеска является предположение о свойстве изотропности турбулентной вязкости потока. Необходимо отметить, что предположение изотропности турбулентного потока является неоправданным при расчетах высокоскоростных вращающихся и закрученных турбулентных течений, а также потоках с развитыми вторичными течениями, вызванными неоднородностью распределения напряжений.
Хотя установленные по умолчанию константы модели турбулентности справедливы для широкого диапозона течений, вы можете поменять их по своему усмотрению в панели Viscous Model.
"RNG" основана на k-e модели турбулентности и получена из точных уравнений Навье-Стокса с использованием математической теории "renormalization group". Модель получена с помощью аналитических методов с различными константами в стандартной k-e модели, и дополнительных условий и функций в уравнениях переноса k и e. Более полное описание "RNG" теории в применении к моделям турбулентности можной найти в [36].
Уравнения переноса в "RNG" k-e модели
Уравнения переноса для k и e имеют следующую форму записи:
|
|
10.4-4 |
|
|
10.4-5 |
В этих уравнениях, 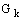 - производство турбулентной
кинетической энергии, вызванное градиентами осредненного потока, способ вычисления описан в секции 10.4.4.
- производство турбулентной
кинетической энергии, вызванное градиентами осредненного потока, способ вычисления описан в секции 10.4.4.
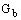 - производство турбулентной кинетической энергии, вызванное
плавучестью, способ вычисления описан в секции 10.4.5.
- производство турбулентной кинетической энергии, вызванное
плавучестью, способ вычисления описан в секции 10.4.5. 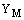 -
параметр характеризующий пульсации вызванные расширением в сжимаемых турбулентных потоках, рассчитывается,
как описано в секции 10.4.6.
-
параметр характеризующий пульсации вызванные расширением в сжимаемых турбулентных потоках, рассчитывается,
как описано в секции 10.4.6. 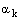 и
и
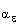 - эффективная инверсия чисел Прандтля для k и e,
соответственно.
- эффективная инверсия чисел Прандтля для k и e,
соответственно. 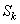 и
и 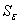 - источники определяемые пользователем.
- источники определяемые пользователем.
Моделирование эффективной вязкости
Согласно особенностям RNG теории необходимо исключить из уравнений длину пути смешения, для чего было выведено дифференциальное уравнение для турбулентной вязкости:
|
|
10.4-6 |
где
 ,
,
Такой подход позволяет более качественно описать явление переноса турбулентности в потоках с малыми числами Рейнольдса и в пристеночных областях. Для больших чисел Рейнольдса турбулентная вязкость, как и раньше, определяется выражением:
|
|
10.4-7 |
где Cm=0.0845, получено в рамках "RNG" теории. Стоит обратить внимание, что значение этого параметра достаточнно близко к значению, полученного опытным путем (0.09), которое используется для стандартной k-e модели.
Во FLUENT, по умолчанию, эффективная вязкость вычисляется с помощью теории полученной для потоков с большим числом Рейнольдса, уравнение 10.4-7. Однако, доступна опция позволяющая вам использовать дифференциальное отношение, уравнение (10.4-6), когда вам необходимо учитывать эффекты низкорейнольдсовых течений.
Учет эффекта закрученности турбулентного потока
Вращение и закрученность осредненного потока оказывают существенное влияние на структуру турбулентности, в частности на турбулентную вязкость. "RNG" k-e модель, реализованная во FLUENT, имеет возможность учета эффектов закрученности и вращения. Для таких потоков турбулентная вязкость имеет следующую функциональную зависимость:
|
|
10.4-8 |
где mt0 - значение турбулентной вязкости, рассчитанное без учета эффектов закрученности и вращения потока по уравнениям (10.4-6), (10.4-7). W является характерным числом закрутки потока, и as - постоянная закрутки, которой присваиваются различные значения в зависимости от того является ли область всего потока закрученной или имеет место средняя (локальная) закрутка потока. Учет эффекта закрученности в "RNG" модели позволяет учитывать эффекты осесимметричных, вращающихся потоков и трехмерных течений. Для потоков с низким эффектом закрутки as=0.05 (установлен по умолчанию во FLUENT) и является фиксированным. Для сильно закрученных потоков коэффициент as имеет более высокое значение (определяется пользователем).
Вычисление эффективной инверсии чисел Прандтля
Эффективные числа Прандтля ak и ae - вычисляются с помощью следующей формулы, полученной аналитически согласно "RNG" теории:
|
|
10.4-9 |
где a0=1.0. При высоких числах Рейнольдса имеет место ограничение
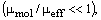
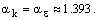
[...]